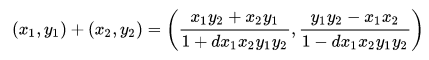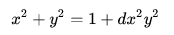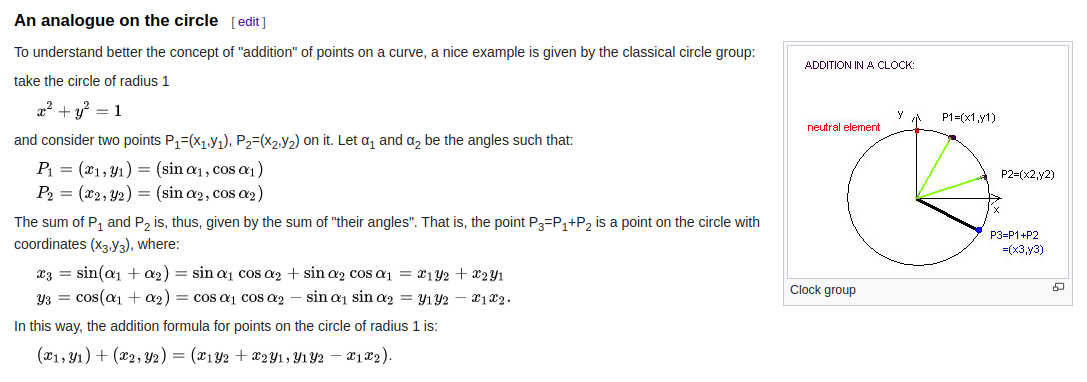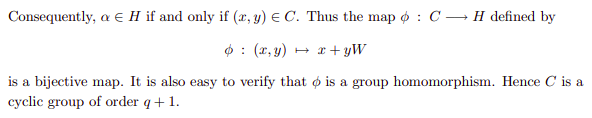m0leCon CTF 2020 Teaser — King Exchange
all images are clickable
The given zip-archive contains two files: a python script and its output.
server.py:
from Crypto.Util.number import long_to_bytes
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
import random
from hashlib import sha256
from secret import flag, p
def add_points(P, Q):
return ((P[0]*Q[0]-P[1]*Q[1]) % p, (P[0]*Q[1]+P[1]*Q[0]) % p)
def multiply(P, n):
Q = (1, 0)
while n > 0:
if n % 2 == 1:
Q = add_points(Q, P)
P = add_points(P, P)
n = n//2
return Q
def gen_key():
g = (0x43bf9535b2c484b67c68cb98bace14ae9526d955732e2e30ac0895ab6ba, 0x4a9f13a6bd7bb39158cc785e05688d8138b05af9f1e13e01aaef7c0ab94)
sk = random.randint(0, 2**256)
pk = multiply(g, sk)
return sk, pk
a, A = gen_key()
b, B = gen_key()
print(A)
print(B)
shared = multiply(A, b)[0]
key = sha256(long_to_bytes(shared)).digest()
aes = AES.new(key, AES.MODE_ECB)
ciphertext = aes.encrypt(pad(flag.encode(), AES.block_size))
print(ciphertext.hex())output.txt:
(70584838528566138057920558091160583247156394376694509226477175997005624, 47208562635669790449305203114934717034939475647594168392271311241505021)
(28274152596231079767179933954556001021066477327209843622539706192176128, 99565893173481261433550089673695177934890207483997197067732588009694082)
aaa21dce78ef99d23aaa70e5d263719de9245f33b8a9e2a0a63c8847dba61296c5a1f56154b062d3a347faa31b8d8030
The encryption algorithm is straightforward: it uses AES-ECB with unknown key and prints out a ciphertext.
aaa21dce78ef99d23aaa70e5d263719de9245f33b8a9e2a0a63c8847dba61296c5a1f56154b062d3a347faa31b8d8030
We need to recover the key, let’s find out how it was generated.
a, A = gen_key() # A = multiply(g, a)
b, B = gen_key() # B = multiply(g, b)
shared = multiply(A, b)[0] # shared = multiply(multiply(g, a), b)[0]The challenge performs some kind of Diffie-Hellman key exchange with unknown modulus p (we will back to this later). It means that server generates two secret values a and b, multiplies the generator g by these secret values and prints out resulting A = g * a and B = g * b.
g = (0x43bf9535b2c484b67c68cb98bace14ae9526d955732e2e30ac0895ab6ba,
0x4a9f13a6bd7bb39158cc785e05688d8138b05af9f1e13e01aaef7c0ab94)
A = (70584838528566138057920558091160583247156394376694509226477175997005624,
47208562635669790449305203114934717034939475647594168392271311241505021)
B = (28274152596231079767179933954556001021066477327209843622539706192176128,
99565893173481261433550089673695177934890207483997197067732588009694082)
The shared key (the same key for AES encryption) is calculated as S = A * b = B * a.
We need to obtain a or b, that means we need to solve a well-known discrete logarithm problem.
The main mystery there is which group we’re working in? Let’s take a closer look on functions multiply and add_points.
def multiply(P, n):
Q = (1, 0)
while n > 0:
if n % 2 == 1:
Q = add_points(Q, P)
P = add_points(P, P)
n = n//2
return Qmultiply(P, n) is a simple double-and-add algorithm for faster P * n multiplication.
def add_points(P, Q):
return ((P[0]*Q[0]-P[1]*Q[1]) % p, (P[0]*Q[1]+P[1]*Q[0]) % p)This P + Q operation is not so obvious (at least at the first sight), but it reminded me the addition law on Edwards elliptic curves:
It brought me to a solution. The d parameter in denominator is a curve parameter which has the form:
If we set d = 0 in the fractions below then we will get our addition algorithm — notice that the both numerators of fractions are equal to our add_points result. But what will happen if we set d = 0 in Edwards curve equation?
That’s right! With d = 0 it becomes just a circle. That case is also mentioned in Wikipedia article:
Ok, now we’ve got the curve we’re working on. A, B and g are points on the circle.
Remember unknown modulus p? Now we are able to recover it. From circle equation we get:
A[0]^2 + A[1]^2 == 1 (mod p)B[0]^2 + B[1]^2 == 1 (mod p)
Move 1 to the left side and rewrite the module condition:
A[0]^2 + A[1]^2 - 1 == k1 * pB[0]^2 + B[1]^2 - 1 == k2 * p
Now p is the common divisor (probably, greatest) of the left sides of the equation. Using Euclidean algorithm we could recover it.
from math import gcd
p = gcd(A[0]^2 + A[1]^2 - 1, B[0]^2 + B[1]^2 - 1)
# p = 108848362000185157098908557633810357240367513945191048364780883709439999The given p is prime, so we’re lucky, it is our modulus! But we still need to solve discrete logarithm.
After some searching I’ve found a question on StackExchange, where the author is asking why we use elliptic curves instead of other curves (such a circle) in cryptography. The answer gives a link to paper with a proof that the discrete logarithm in the circle group is no stronger than the discrete logarithm over the underlying field.
There was suggested a map (paragraph 3) from a circle group to Fp[W]/(W^2 + 1) (where Fp = GF(p)):
So I’ve tried to rewrite it in sage and run standart discrete_log function.
F = GF(p)
R.<w> = PolynomialRing(F)
K.<w> = F.extension(w^2 + 1)
g_K = g[0] + g[1]*w
B_K = B[0] + B[1]*w
b = discrete_log(B_K, g_K)
print(b)
print(multiply(g, b) == B)
# 84409516282208830711822012296755714894563394060577082225590467549929629
# TrueWe’re lucky again, after some seconds it was printed the secret b! In the general case we would need to check smoothness of the field order and other parameters, but here it’s not required — sage did its job.
Now we easily can calculate shared key and decrypt the flag:
shared = multiply(A, b)[0]
key = sha256(long_to_bytes(shared)).digest()
aes = AES.new(key, AES.MODE_ECB)
plaintext = aes.decrypt(bytes.fromhex(ciphertext))
print(plaintext)The flag is ptm{c1rcl3s_r_n0t_4s_53cur3_4s_ell1ps3s}.