CONFidence CTF 2020 Finals — ElGamal
all images are clickable
Challenge sources
The given tar-archive contains two files:
- Challenge.cabal — challenge package description designed in Cabal:
name: Challenge
version: 0.1.0.0
build-type: Simple
cabal-version: >=1.10
executable Challenge
main-is: Main.hs
build-depends: base,
arithmoi,
bytestring,
cryptonite,
crypto-api,
safe
default-language: Haskell2010
- Main.hs — server source code written in Haskell:
import Control.Exception
import Control.Monad
import Crypto.PubKey.ECC.Types
import Crypto.PubKey.ECC.Prim
import Crypto.Util
import qualified Data.ByteString as B
import Data.Foldable
import Data.Maybe
import Math.NumberTheory.Primes
import Math.NumberTheory.Moduli.Sqrt
import Safe
import System.IO
curve = getCurveByName SEC_p256k1
curve_fp = case curve of CurveFP cfp -> cfp
p = ecc_p curve_fp
pp = fromJust (isPrime p)
a = ecc_a $ common_curve curve
b = ecc_b $ common_curve curve
main :: IO ()
main = do
hSetBuffering stdout NoBuffering
x <- scalarGenerate curve
let h = pointBaseMul curve x
putStrLn $ "I, Giorno Giovanna, have an ElGamal public key: " ++ show h
result <- try $ sequence_ $ replicate 5 $
menu [("Encrypt", encrypt h),
("Decrypt", decrypt x),
("Get flag", userAskedForFlagLol x)]
case result of
Left (ErrorCall msg) -> putStrLn $ msg ++ ". Bye!"
Right _ -> putStrLn "Okay, that's enough. I ain't got all day."
encrypt :: Point -> IO ()
encrypt h = do
putStr "Message: "
msg <- B.getLine
y <- scalarGenerate curve
let s = pointMul curve y h
putStrLn $ "c1: " ++ show (pointBaseMul curve y)
putStrLn $ "c2: " ++ show (pointAdd curve (encodeMessage msg) s)
decrypt :: PrivateNumber -> IO ()
decrypt x = do
putStr "c1: "
c1 <- readLn
unless (isPointValid curve c1) $ do
return (error "Point invalid")
putStr "c2: "
c2 <- readLn
unless (isPointValid curve c2) $ do
return (error "Point invalid")
let s = pointMul curve x c1
let s_inv = pointNegate curve s
let m = pointAdd curve c2 s_inv
print (decodeMessage m)
userAskedForFlagLol x = do
putStrLn "Now, why would I ever give you that?"
input <- readLn
if input == x
then do
putStrLn "Ho... how did you get that?! I guess I have no choice..."
flag <- readFile "flag.txt"
putStrLn flag
-- Not an error, but it's the easiest way to bail
error "I hope you're happy"
else do
error "I knew you wouldn't convince me"
menu :: [(String, IO ())] -> IO ()
menu options = do
putStrLn "What would you like to do?"
foldM_ showOption 1 options
choice <- readLn
case atMay options (choice - 1) of
Just (_, op) -> op
Nothing -> error "That does not look like one of the options"
where
showOption index (name, _) = do
putStrLn $ "[" ++ show index ++ "] " ++ name
return $ index + 1
encodeMessage :: B.ByteString -> Point
encodeMessage = encodeInteger . bs2i
decodeMessage :: Point -> B.ByteString
decodeMessage = i2bs_unsized . decodeInteger
discardBits = 8
maxMessage = p `div` 2^discardBits
encodeInteger :: Integer -> Point
encodeInteger n
| n > maxMessage = error "Message too long"
| n == maxMessage = PointO
| otherwise =
case asum [findY $ n * 2^discardBits + k | k <- [0..2^discardBits-1]] of
Just p -> p
Nothing -> error "Go play the lottery or something"
decodeInteger :: Point -> Integer
decodeInteger PointO = maxMessage
decodeInteger (Point x y) = x `div` 2^discardBits
findY :: Integer -> Maybe Point
findY x = Point x <$> listToMaybe (sqrtsModPrime (x^3 + a*x + b) pp)Analyzing source code
Let’s look on these files.
First we’ll consider that Cabal package file may be useful later, when we would run the Haskell application locally. So we will start analyzing the Haskell code. Since it’s a bit unusual to see Haskell code in the crypto challenge, the reading itself isn’t too hard. After spending a few minutes I could slightly understand what’s going on.
Okay, so we’re working with some Elliptic curve. The analysis of encrypt/decrypt functions (or just reading the challenge’s name) helps us to guess the encryption scheme — it’s ElGamal. So, here is ElGamal scheme over the Elliptic curve, right? Yea, looks secure, because discrete logarithm problem is still hard on Elliptic curves (this probem is also known as ECDLP).
The curve is secp256k1, it’s a well-known Elliptic curve, and it provides enough security for this challenge. This curve is even used by Bitcoin. Since we’re working over that curve, let’s start our exploit with curve parameters. We denote the curve E and its base point G:
#!/usr/bin/env sage
p = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F
F = GF(p)
E = EllipticCurve(F, [0, 7])
G = E(0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798,
0x483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8)I’ll describe a bit what the server does:
-
First it generates an integer
x— ElGamal private key. Next it computesH = x * G(whereGis the curve base point) and prints outH— ElGamal public key. Since we know the curve, we know all the parameters, except forx. Our goal is find outxand break the cryptosystem. -
Then the server gives us 5 attempts to encrypt and decrypt arbitrary messages. We also could ask for the flag, but we need to know the private key. When we send correct
xto the server, it will print the flag. But if ourxis invalid, the server drops the connection. -
How does the server stores a message inside the Elliptic curve? It just transforms it into the Elliptic curve point! Suppose we have an integer
M— our message. Server considersMas a part of point’s X-coordinate: it multipliesMby 256 and bruteforces the least significant byte, until it get the correct X-coordinate. Pseudocode:
M = <our message>
for i in range(256):
x = M * 256 + i
if secp256k1 contains a point with such x:
return (x, y)
- Retrieving message process is similar: the server just takes the X-coordinate and divides it by 256. But there was some unexpected text-encoding of non-printable characters. For example:
"])\229\243Jb)L\200\163\139\239\236U:\ENQ&t\RSH5,\152a\233\227\DC4)\bf\221". I don’t know what it is, so my teammate @ilyaluk helped me and wrote the decoder:
def unescape(s):
ascii_controls = [
(b'\\a', b'\x07'),
(b'\\b', b'\x08'),
(b'\\f', b'\x0C'),
(b'\\n', b'\x0A'),
(b'\\r', b'\x0D'),
(b'\\t', b'\x09'),
(b'\\v', b'\x0B'),
(b'\\"', b'\x22'), # ???
(b'\\\'', b'\x27'), # ???
(b'\\\\', b'\x5C'), # ???
(b'\\NUL', b'\x00'),
(b'\\SOH', b'\x01'),
(b'\\STX', b'\x02'),
(b'\\ETX', b'\x03'),
(b'\\EOT', b'\x04'),
(b'\\ENQ', b'\x05'),
(b'\\ACK', b'\x06'),
(b'\\BEL', b'\x07'),
(b'\\BS', b'\x08'),
(b'\\HT', b'\x09'),
(b'\\LF', b'\x0A'),
(b'\\VT', b'\x0B'),
(b'\\FF', b'\x0C'),
(b'\\CR', b'\x0D'),
(b'\\SO', b'\x0E'),
(b'\\SI', b'\x0F'),
(b'\\DLE', b'\x10'),
(b'\\DC1', b'\x11'),
(b'\\DC2', b'\x12'),
(b'\\DC3', b'\x13'),
(b'\\DC4', b'\x14'),
(b'\\NAK', b'\x15'),
(b'\\SYN', b'\x16'),
(b'\\ETB', b'\x17'),
(b'\\CAN', b'\x18'),
(b'\\EM', b'\x19'),
(b'\\SUB', b'\x1A'),
(b'\\ESC', b'\x1B'),
(b'\\FS', b'\x1C'),
(b'\\GS', b'\x1D'),
(b'\\RS', b'\x1E'),
(b'\\US', b'\x1F'),
(b'\\SP', b'\x20'),
(b'\\DEL', b'\x7F'),
]
for fr, t in ascii_controls:
s = s.replace(fr, t)
for i in range(256):
s = s.replace(b'\\' + str(i).zfill(3).encode('ascii'), bytes([i]))
return sSo, now we completely understand what the server does. Let’s try to find some vulnerabilities.
Invalid curve attack
There are no obvious vulnerabilities, because secp256k1 is secure itself, and the code ensures all required security checks. Since we need to recover x, I started to analyze decrypt function, because it was the only one place in the whole code where x is used. Here is decrypt pseudocode:
def decrypt(x):
c1 = input point
assert c1 is on secp256k1
c2 = input point
assert c2 is on secp256k1
s = x * c1
s_inv = -s
m = c2 + s_inv # c2 - s
return m
Luckily, we control the point c1, which are multiplied by x! Looks like a clue. Since we know c1, c2 and resulting m, we can reverse all transformations and retrieve s. But discrete logarithm is still hard.
First I started to think about Small subgroup attack, but quickly realized that the curve base point G has prime order (quite expected). Suddenly my teammate @CerebralObserver pointed out that some security check does not hold! More precisely, this code just does nothing (I don’t know Haskell, so I don’t understand why, but it’s a fact). These errors are never thrown:
putStr "c1: "
c1 <- readLn
unless (isPointValid curve c1) $ do
return (error "Point invalid")
putStr "c2: "
c2 <- readLn
unless (isPointValid curve c2) $ do
return (error "Point invalid")
When we’re working with Elliptic curves, we need to ensure that all points are on the curve. It means if we have a point (x0, y0) we need to check the equation y0^2 == x0^3 + a*x0 + b (where y^2 == x^3 + a*x + b is our Elliptic curve). If the equation does not hold (or we just don’t check it), the cryptosystem becomes vulnerable to Invalid curve attack.
This attack exploits the fact that we are able to send fake point to the server, and it will perform all Elliptic curve operations with our fake point. To understand the attack, let’s look at the Elliptic curve addition law. If we want to calculate R = P + Q, here are two main cases:
P != Q
s = (P.y - Q.y) / (P.x - Q.x)
R.x = s ^ 2 - P.x - Q.x
R.y = P.y + s * (R.x - P.x)
P == Q
s = (3 * P.x ^ 2 + a) / (2 * P.y)
R.x = s ^ 2 - 2 * P.x
R.y = P.y + s * (R.x - P.x)
As you see, the addition law uses at most a coefficient from the Elliptic curve equation, and b is never used! So without the correct curve check we could send a fake point from another Elliptic curve (with another b coefficient)! Thats why the attack called Invalid curve — we send a fake point from Invalid (less secure) curve, but the secret remains the same. Using known vulnerabilities in our Invalid curve we could “easily” find the discrete logarithm.
Mapping to additive group
How Invalid curve attack could be exploitable in our case? Let’s look at the secp256k1 equation again:
y^2 = x^3 + 7 (mod 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F)
See this? a == 0! And we also could make b == 0, using Invalid curve attack. With a == 0 and b == 0 our equation becomes “more simple”:
y^2 = x^3 (mod 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F)
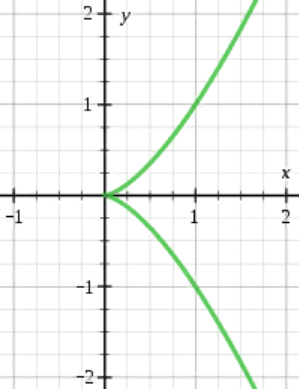
So, we can send a point from a cusp:
Cusp has well-known property, which becomes useful in our case. One can construct a map from the cusp to an additive group. And the discrete logarithm in an additive group is just division:
source: https://crypto.stackexchange.com/a/67120
So our plan is:
- Send a point
c1 = Point 1 1,c2 = PointO(point at infinity) - Receive
-s = -(x * c1). SetQ = -s(using guessing a point Y-coordinate with 1-byte bruteforce) - Calculate
x = -(Q.x / Q.y)(wherexis private key) - Send
xand get the flag!
Final exploit
#!/usr/bin/env sage
import socket
p = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F
F = GF(p)
E = EllipticCurve(F, [0, 7])
G = E(0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798,
0x483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8)
def unescape(s):
ascii_controls = [
(b'\\a', b'\x07'),
(b'\\b', b'\x08'),
(b'\\f', b'\x0C'),
(b'\\n', b'\x0A'),
(b'\\r', b'\x0D'),
(b'\\t', b'\x09'),
(b'\\v', b'\x0B'),
(b'\\"', b'\x22'), # ???
(b'\\\'', b'\x27'), # ???
(b'\\\\', b'\x5C'), # ???
(b'\\NUL', b'\x00'),
(b'\\SOH', b'\x01'),
(b'\\STX', b'\x02'),
(b'\\ETX', b'\x03'),
(b'\\EOT', b'\x04'),
(b'\\ENQ', b'\x05'),
(b'\\ACK', b'\x06'),
(b'\\BEL', b'\x07'),
(b'\\BS', b'\x08'),
(b'\\HT', b'\x09'),
(b'\\LF', b'\x0A'),
(b'\\VT', b'\x0B'),
(b'\\FF', b'\x0C'),
(b'\\CR', b'\x0D'),
(b'\\SO', b'\x0E'),
(b'\\SI', b'\x0F'),
(b'\\DLE', b'\x10'),
(b'\\DC1', b'\x11'),
(b'\\DC2', b'\x12'),
(b'\\DC3', b'\x13'),
(b'\\DC4', b'\x14'),
(b'\\NAK', b'\x15'),
(b'\\SYN', b'\x16'),
(b'\\ETB', b'\x17'),
(b'\\CAN', b'\x18'),
(b'\\EM', b'\x19'),
(b'\\SUB', b'\x1A'),
(b'\\ESC', b'\x1B'),
(b'\\FS', b'\x1C'),
(b'\\GS', b'\x1D'),
(b'\\RS', b'\x1E'),
(b'\\US', b'\x1F'),
(b'\\SP', b'\x20'),
(b'\\DEL', b'\x7F'),
]
for fr, t in ascii_controls:
s = s.replace(fr, t)
for i in range(256):
s = s.replace(b'\\' + str(i).zfill(3).encode('ascii'), bytes([i]))
return s
def read_public_key(file):
text = b'I, Giorno Giovanna, have an ElGamal public key: '
line = file.readline().strip().decode()
point_info = line[len(text):].split(' ')
return tuple(map(int, point_info[1:]))
def decrypt_message(file, c1, c2):
text = b'c1: c2: '
file.write(f'2\n{c1}\n{c2}\n'.encode())
file.flush()
for _ in range(4):
file.readline()
return file.readline()[len(text):].strip()[1:-1]
def get_flag(file, x):
file.write(f'3\n{x}\n'.encode())
file.flush()
for _ in range(6):
file.readline()
return file.readline().strip().decode()
def main(address):
while True:
with socket.socket(socket.AF_INET, socket.SOCK_STREAM) as sock:
sock.settimeout(3)
sock.connect(address)
file = sock.makefile('rwb')
H = E(read_public_key(file))
message = decrypt_message(file, 'Point 1 1', 'PointO')
_x = int.from_bytes(unescape(message), 'big')
for dx in range(256):
x = F(_x * 256 + dx)
if not (x ^ 3).is_square():
continue
y = (x ^ 3).sqrt()
secret = int(-(x / y))
if secret * G == H:
print(get_flag(file, secret))
return
if __name__ == '__main__':
# main(('0.0.0.0', 31337))
main(('elgamal.zajebistyc.tf', 13403))Flag: p4{t0O_l4zy_t0_ev@luat3_th3_many_p0ss1bl3_j0k3s_I_c@n_m@k3_h3r3}
Many thanks to the author, the challenge is great!